考虑库存费用的多约束排产优化研究

　　0 引言

    　市场经济条件下，面向订单的企业生产计划是一个多目标决策，要同时考虑客户、企业和市场等多方面的要求。在以上多目标决策过程中，库存和排产优化同等重要，因此怎样在排产优化中使库存既能发挥调节供需平衡的作用又能尽量减少维护费用，是一个值得研究的课题。

    　与企业实际生产相结合，排产问题有多型号生产线、有限产能、客户交货时间要求等多种约束，同时还要考虑库存费用，优化过程比较复杂。在可查找的文献来看，很少见到考虑库存费用的多约束排产优化研究成果。本文将以作者研究的某大型企业实际生产过程为背景，提出一种分层遗传算法对排产问题进行寻优，最后以该企业一个实际的排产算例结果及其分析来说明本文算法的有效性。

　　1 考虑库存费用的多约束排产优化

    　一般企业生产分销流程如下图1所示。

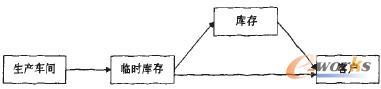
图1 企业生产分销图

   　 临时库存一般设在车间或者离车间很近的地点，临时库存作为生产和库存的中间环节，存放时间较短，周转率高。因此当货物交货期离生产期时间比较长时，需要把产品转入到正式库存，这个过程的费用包括货物运输费用、库存维护费用以及仓库租用费用等。因此，如何有效进行排产，既能满足交货期的要求又能减少库存费用，是本文研究的主题。

    　考虑库存费用的多约束排产优化问题可以描述如下：

   　 1)企业有多条不同的生产线，每条生产线能生产一种或多种产品，不同的生产线对不同产品的产能各不相同，各生产线运营成本不同。

    　2)在计划期内，要对多个客户订单进行排产。每个客户订单含有多个型号的产品及数量。

   　 3)每个客户订单对各型号产品都有交货时间要求，违期要交不同数量的违约金。

  　  4)临时库存有存放货物数量上限约束，存放时间上限约束；当某产品的生产时间和交货时间的间隔超过临时库存时间上限时，需要转入到正式库存。

   　 5)存储费用包括货物转入正式库存需要运输费用和库存维护费用。

   　 决策目标为生产该批产品的生产线运营费用、客户违约费用和存储费用最小。

　　2 分层遗传算法设计

　　2.1 分层遗传算法

 　   遗传算法(genetic algorithm，简称为GA)是基于。适者生存”的一种高度并行、随机和自适应化的优化算法，它通过模拟物种的进化过程达到寻求整体最优的目标。普通遗传算法是首先产生一个初始种群，通过设计的进化操作来对问题求解。普通遗传算法往往导致遗传种群缺乏多样性而过早的收敛。

  　  分层遗传算法(Hierarchic Genetic Algorithm，简称HGA)是对上述遗传算法的改进。HGA首先进行低层遗传算法操作：生成多个初始种群，各种群设置不同的参数独立的进行各自的遗传算法，当各种群进化到一定程度，进入到高层遗传算法操作：将各种群的平均适应度作为种群适应度，进行以种群为单位的进化操作。HGA通过在底层遗传算法阶段获得位于个体串的一些特定位置的优良模式，通过高层遗传算法阶段获得包含不同种类的优良模式的新个体，从而得到较好的寻优效果。

　　2.2 染色体编码设计

   

　　2.3 低层遗传算法阶段操作

    　2.3.1 初始群体的产生

    　低层遗传算法阶段初始群体的产生步骤为：从编码位置1开始到位置，结束，首先确定能生产该位置产品的生产线集合，然后在这个集合中随机选择一条生产线，把该生产线的编码写入当前位置；重复以上过程N次，得到规模为N的初始群体。重复以上产生群体的的过程M次，得到M个种群规模为N的初始群体。

   　 2.3.2 交叉操作

    　采用多点交叉操作。多点交叉的思想源于控制个体特定行为的染色体表示信息的部分无须包含于邻近的字串中，多点交叉的破坏性可以促进解空间的搜索，而不是促进过早的收敛，因此搜索更加健壮。多点交叉步骤为：随机选择m个交叉位置，除了第一位变量与第一个交叉点之间的一段不做交换外，其它交叉点之间的变量可以间续的相互交换，产生两个新的后代。

   　 2.3.3 变异操作

    　采用多次2-swap变异。一旦遂机数小于变异概率，则变异操作发生，随机选取两个基因进行交换，当遇到不能交换的基因时，取消交换操作，重新选择交换基因，直到能够进行变异。

　　2.4 高层遗传算法阶段操作

  　  2.4.1 选择操作

   　 计算低层遗传算法阶段得到的M个种群的平均适应度值，根据平均适应度值用轮盘赌方法进行选择。

   　 2.4.2 交叉操作

  　  与低层染色体交叉不同，高层遗传算法是对种群进行操作。本文采用的方法是：当两个父代种群被匹配在一起进行交叉操作，随机选择两个交叉点X1，X2，然后交换这两个父代种群中区[x1，x2]间的染色体。

　    2.4.3 变异操作

 　   高层遗传算法的变异操作是群体进行小概率改变的操作。本文采用的方法是：以随机生成的新个体小概率替换抽取的群体中某个体。

　　2.5 约束的处理及适应度函数

 　   本文考虑库存费用的多约束排产优化问题包含的约束有生产线生产产品的型号约束、各订单的交货期限约束和临时库存最长存货时间限制。对于生产线生产产品的型号约束，本文在初始群体的产生、GA交叉、变异操作中已经得到了控制。对于各订单的交货期限约束和临时库存最长存货时间限制，本文采取在适应度函数中增加惩罚值的方法。适应度函数可用如下公式表示。

   

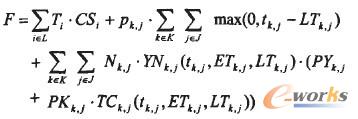
    　上式中L表示生产线的集合；

    　Ti表示生产线i的生产时间；

    　CSi表示生产线i单位时间的运营费用；

    　Pkj表示订单k中产品j的延期交货的单位时间违约费用；

   　 tkj表示订单k中产品j的实际生产完成时间；

   　 LTkj表示订单k中产品j的最晚交货时间；

    　ETkj表示订单k中产品j的最早交货时间；

  　  TCkj(tkj，ETkj，LTkj)为订单k中产品j存入库存的时间长度，它是tkj，ETkj，LTkj的函数。

   

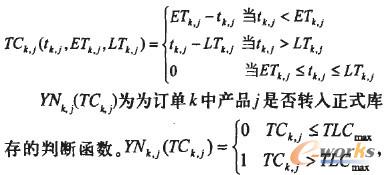
   　 TLCmax为临时库存最大存放时间。

   　 Nkj为订单k中j产品的数量；

    　PYkj为订单良k中产品j转入正式库存的单位运输费用；

    　Pkj为订单k中产品j单位库存维护费用；

    　TCkj(tkj，ETkj，LTkj)为订单k中产品j存入库存的时间长度，它是的函数。

   

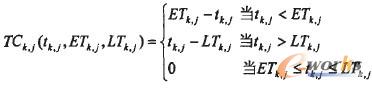
　　2.6 终止准则

   　 本文HGA包括3个终止准则：低层终止准则、高层终止准则和算法终止准则。低层终止准则即什么时候跳出低层进化阶段，高层终止准则即什么时候跳出高层进化阶段，算法终止准PPJep结束整个算法的条件。对于底层和高层终止准则，本文采用采用最大循环代数终止准则。算法终止准则采用的是最优解没有改进的最大进化代数。

　　2.7 HGA框架

    　考虑库存费用的多约束排产优化HGA框架如图2所示。

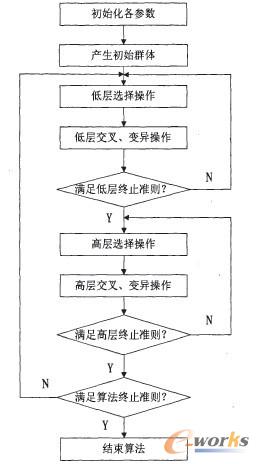
图2 考虑库存费用的多约束排产优化HGA框架

　　3 试验结果及分析

　　3.1 试验结果

   　 把本文应用于作者在研的一个实际企业生产项目，对某高新技术企业的玻壳生产线的排产过程进行优化。企业有玻壳生产线27条，每条生产线能生产一种或几种产品。选取订单规模较大的一次，对23份订单总共36种产品数量达170．6万个产品进行优化。

 　   运算20次，平均计算时间为6分49秒，得到了令人满意的结果，解的最大波动幅度为3．5％。由于企业当前系统不能进行如此复杂的优化(该企业对如此规模定单一般是人工排产)，故不好直接比较本文算法与该系统性能的优劣，但是从实用角度分析，对如此大规模的订单排产问题，本算能在较短的时间内完成优化，稳定性好，结果令人满意，证明本文HGA是优化考虑库存费用的多约束排产问题的有效算法。

　　3.2 比较试验

  　  为了体现本文的优势，我们把本文提出的HGA与普通遗传算法对3.1算例结果进行比较，分别进行20次运算，得到如下表1的结果。

表1 比较试验结果

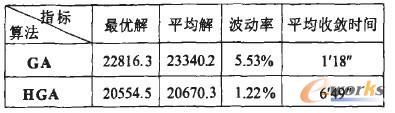
    　从表1可以看出：对比普通遗传算法，本文HGA在寻优能力和计算稳定性方面都有较大优势。但是由于HGA是分两层循环进行优化，这是以牺牲收敛速度为代价的，因此普通遗传比HGA速度快，但是HGA对于数量达170．6万个产品的大型订单进行排产，能在7分钟之内完成优化，且最优结果比普通遗传算法节省成本达11．0％，因此，无论从试验还是实用角度分析，HGA优化结果都是令人满意的。

　　4 结束语

    　本文对考虑库存费用的多约束排产优化问题进行了描述，提出了优化该问题的分层遗传算法。本文详细介绍了此算法的原理，通过一实际订单的优化计算及与普通遗传算法得到的结果进行比较，证明了本文提出的HGA对考虑库存费用的多约束排产优化问题的有效性。

(本文不涉密)
责任编辑：

转载：感谢您对网站平台的认可，以及对我们原创作品以及文章的青睐，非常欢迎各位朋友分享到个人站长或者朋友圈，但转载请说明文章出处。