用PCL语言增强MSC Patran三角网格划分功能

0 引 言

    以实体建模包括基于特征的参数化建模和空间自由曲面混合造型两种方法为代表的CAD 软件对表面形态的表示法已经大大超过了CAE 软件利用CATIA PRO/E 等CAD 平台完成船体部件模型设计借助于MSC Patran 进行有限元划分使用MSCNastran 进行求解分析已是一种实用的方法. 模型在这两类软件传递过程中曲线与曲面的空间位置即几何图形传递比较容易而图形数据的逻辑关系即拓扑关系的传递经常出现局部失败情况导致导入CAE 的模型包含细小的孔狭窄的槽甚至是建模过程中形成的小曲面等. 对于导入的模型和已建立的复杂模型在使用有限元方法求解强度问题之前修补模型以及有限元网格划分是有限元数值模拟分析至关重要的一步它直接影响着后续数值计算分析结果的精确性.

1 网格划分修补流程图

2 发现缝隙

    对于一个没有缝隙的三角网格模型任意一条边属于两个三角网格. 如果存在某条边仅属于一个三角网格则该条边是构成缝隙多边形的一条边即边界边如果某条边属于两个三角网格则称该条边为内部边. 由边界边首尾相连组成的封闭空间多边形称为缝隙缝隙在一些文中称为孔洞. 在使用MSC Nastran 求解时这些缝隙的存在往往会导致计算不收敛因此在提交求解器有限元分析前对缝隙进行修补是必须的. 网格模型的缝隙修补问题已有不少学者进行了深入的研究.一般来说使用MSC Patran划分网格后缝隙相对于有限元单元来说是很少的且每个缝隙组含有少量的节点基于这种情况对带有缝隙的整船三角网格模型首先将缝隙分类根据不同的类别使用对应的的网格修补优化的方法.

3 缝隙分类修补及优化

    3.1 建立缝隙邻接矩阵和确定搜索算法

    从结构模型中搜索并形成缝隙的节点集合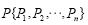和与缝隙相关联的三角网格集合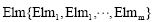,得知整船三角网格模型的缝隙连通邻接矩阵A 为nxn 的上下三角对称矩阵.对每一个与缝隙相关的节点Ni,在与该缝隙相关的有限元网格Elm中查找. 缝隙上的Pi和Pj两个节点连通的权值

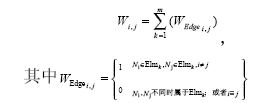
    则所有求得缝隙相关连通邻接矩阵

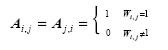
    对邻接矩阵的每一个节点Pi,其节点度为 一般来说前面经过网格划分后,缝隙组数远远小于三角网格数,即有e << n2,邻接矩阵为稀疏矩阵. 为了提高存储利用率,在物理上使用邻接表数据结构存储. 一个合适的遍历方法应该是针对全体数据集. 而对于图有两种遍历方法:深度优先搜索DFS (Depth First Search) 和广度优先搜索BFS (Breadth First Search). 若图中有n个节点、e条边,且使用邻接表存储稀疏矩阵. 在DFS中,沿邻接链可以找到某个节点P 的所有邻接节点Q,由于共有2e个边节点,所以扫描边的时间为O(e),而对所有节点递归访问1次,所以遍历该图的时间复杂性为O(n+e). 在BFS中,每个节点在搜索时访问且只访问一次,且总时间代价为TD1+TD2+ +TDn=O(e), 其中TDi为节点i的度. 可知BFS 算法更适合对该邻接矩阵的遍历.

 3.2  3个节点组成的缝隙修补以及优化

    3个节点组成的类缝隙直接采用最小内角最大化的准则,使得两个相邻三角形构成的严格凸四边形区域使三角形形状最优的对角线连接方式. 根据节点计算获得缝隙中的最大边emax 和最小边emin 网格内角Anglemax 和Anglemin 并从三角网格集合s2找出和这两个边关联的三角网格。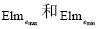

    如果emin <emax /5 且emin <网格尺寸/5，则删除小边emin 相关单元Elmemin且合并emin 的两个节点见图2.

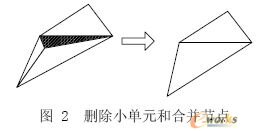
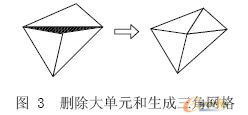
    如果网格内角Anglemax>135°或者Anglemin<15°则删除缝隙中emax 相关的单元Elmemax 形成一个4个点的缝隙,连接Elmemax 的第3点和缝隙中的第3点生成两个三角网格见图3.

    3.3  3个节点以上组成的缝隙修补及优化

    目前,用曲面网格重建算法生成网格,方法分为基于表面法和基于体积法的网格重建算法,HOPPE等人提出将拓扑重建与几何重建同时完成构造一张隐式逼近的三角形分段曲面的方法. Nuid 借鉴HOPPE 算法的思想,提出一种3D 散乱数据点的空间三角剖分算法,文中采用对NUID 改进了的3D 离散数据点的空间三角网格生成算法思想进行三角网格重建. 初始三角网格采用与缝隙相关的一个三角网格Elmemax,以Elmemax任意一边e = (P1 ,P2 ) 为当前边添加其他三角网格定义e 的k-邻域为Nbhd(e) =Nbhd(P1)Y Nbhd (P2) 下一个三角形的最佳顶点必定在Nbhd (e)内. 搜索最佳点的算法如下:

    Step1. 把Nbhd(e) 中的点投影到微切平面

    (P-C)·nc=0 上,nc当前边的邻域的质心点法向量.并令cosmin=2,c nref = nc.

    Step2. 取出Nbhd (e) 投影点集中的一个没有测试的点P3计算该点处夹角的余弦即:

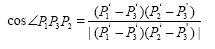
    如果cos∠P1P3P2< cosmin, cosmin = cos∠P1P3P2,

    则P3为最佳点,生成三角网格P1P2P3. 将邻域搜索完毕且cos∠P1P3P2<cosmin不成立,则换一个边e重新开始.

4 总 结

    文中对于在CATIA 设计的整船模型导入MSCPatran 后产生很多小曲面而不能划分有限元网格的情况下对传统的三角网格重建方法进行了改进,根据自由边发现缝隙,提出并使用邻接矩阵的方式对三角网格间的缝隙分类,对分类后的缝隙进行拆分修补,最后通过合并、删除冗余等生成三角平面网格并进行优化. 使得带有“毛刺”的复杂模型可以在MSC Patran 中能进行有限元划分。

转载：感谢您对网站平台的认可，以及对我们原创作品以及文章的青睐，非常欢迎各位朋友分享到个人站长或者朋友圈，但转载请说明文章出处。